MESURE DU RAYON DE LA TERRE : Mesure du rayon de la Terre

MESURE DU RAYON DE LA TERRE ( Eratosthène )
ACTIVITE 2 : Mesure du rayon de la Terre ( suite )

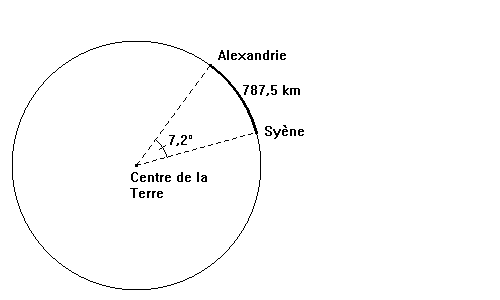
4° Relation entre longueur d'un arc et angle au centre.

Nous savons donc que l'angle au centre de Terre vaut 7,2° et que la longueur de l'arc reliant Syène à Alexandrie est de 787,5 km.

Dans l'activité suivante, nous considérons un cercle ( de rayon égal à environ 3,8 cm ).
En prenant le point A, fais varier la mesure de l'angle puis note les longueurs de l'arc.
Appuie alors sur le bouton "Vérifier".

Angle : | | | | |
_____________________________________________

Longueur de l'arc : | | | | |

( N'indique pas l'inité : cm )

Que remarque-t-on ?

5° périmètre de la "Terre" ( longueur d'un parallèle ).

Revenons maintenant à la Terre et aux mesures effectuées par Eratosthène ( à un angle de 7,2° correspond une longueur d'arc de 787,5 km ) :

On peut alors compléter le tableau suivant, afin de faire apparaître le "périmètre de la Terre" dans la deuxième colonne :

Angle au centre(°) | | |
______________________________

Longueur de l'arc | | |<--- périmètre en km ici ( sans unité )!
( en km )

6°. Calcul du rayon de la Terre

Si on appelle p le périmètre de la Terre, et R son rayon, quelle est la relation entre R et p ?

Ici, on a p = km. Donc :

R = = à 100 km près ;

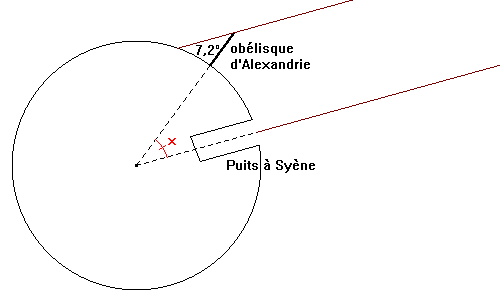
7°. Bilan final de l'activité

Clique sur la figure pour un résumé de l'activité

Tout d'abord, on savait que l'angle entre l'obélisque et les rayons du soleil était de 7,2°.