|
Quelques
DEFIS... |
|
|
Je
vous propose quelques petits défis dont le but est de vous montrer
que le "chapitre" sur les quadrilatères ne permet pas,
à lui seul, de déterminer la nature d'un quadrilatère. Toutes les figures sont des figures réalisées à main levée. Il faudra vous fier uniquement au codage de chaque figure. Enfin, l'avant-dernier exercice devrait donner du fil à retordre aux plus mordus d'entre vous... |
|
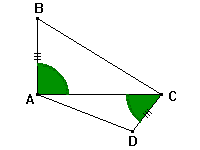 |
Un petit exercice simple pour commencer... Quelle est la nature de ce quadrilatère ? Il faut évidemment le démontrer ! |
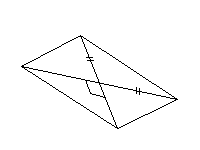 |
Ce
quadrilatère n'est pas un parallélogramme ( item 6 de
l'exercice de reconnaissance visuelle ).
|
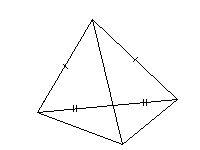 |
Ce
quadrilatère n'est pas un parallélogramme ( item 8 de l'exercice
de reconnaissance visuelle ). Quelle autre condition serait nécessaire pour que ce soit un parallélogramme ? Et si cette condition était remplie, quelle serait alors la nature de ce parallélogramme ? |
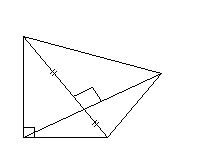 |
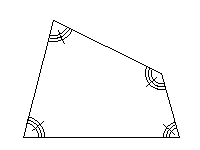
Ce
quadrilatère n'est pas un parallélogramme ( item 14 de
l'exercice de reconnaissance visuelle ). |
 |
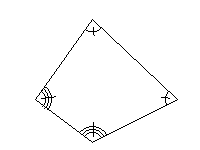
Quelle est la nature de ce quadrilatère ? ( item 15 ) Si vous avez utilisé l'aide à la résolution de l'exercice, vous avez pu en déduire facilement que ce quadrilatère était un parallélogramme. Mais le logiciel ne vous a rien appris de plus ! En fait, le cours sur les parallélogrammes ne suffit pas à lui seul pour déterminer à coup sûr la nature d'un quadrilatère. Faites alors appel à vos connaissances du cours... |
 |
Démontrer que ce quadrilatère est un trapèze. Si ce quadrilatère était un parallélogramme, quelle serait la nature de ce parallélogramme ? |
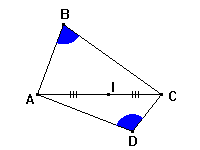 |
Sur cette figure à main levée, I est le milieu de [AC] et les angles en B et en D ont la même mesure. Si l'on suppose en plus que les points B,I,D sont alignés, il est possible de démontrer que ABCD est un parallélogramme . Cet exercice est vraiment délicat au collège. Mais si vous êtes en 4ème et que vous avez déjà étudié le raisonnement par contraposée, vous devriez pouvoir venir à bout de cet exercice... ( pas en 5 minutes, je vous le concède ! ) |
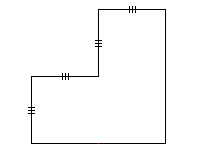 |
Et enfin, juste pour rire ... ( lisez bien cette énigme avant de visualiser l'une des solutions possibles ) Mes
côtés sont deux à deux parallèles, mes angles
sont droits, je possède de plus quatre côtés de
même longueur, et pourtant, je ne suis pas un carré.
En fait, je ne suis même pas un parallélogramme
.Mais qui suis-je donc ?
|
